Apple’s Mysterious Fisheye Projection

If you’ve read my first post about Spatial Video, the second about Encoding Spatial Video, or if you’ve used my command-line tool, you may recall a mention of Apple’s mysterious “fisheye” projection format. Mysterious because they’ve documented a CMProjectionType.fisheye enumeration with no elaboration, they stream their immersive Apple TV+ videos in this format, yet they’ve provided no method to produce or playback third-party content using this projection type.

Additionally, the format is undocumented, they haven’t responded to an open question on the Apple Discussion Forums asking for more detail, and they didn’t cover it in their WWDC23 sessions. As someone who has experience in this area – and a relentless curiosity – I’ve spent time digging-in to Apple’s fisheye projection format, and this post shares what I’ve learned.

As stated in my prior post, I am not an Apple employee, and everything I’ve written here is based on my own history, experience (specifically my time at immersive video startup, Pixvana, from 2016-2020), research, and experimentation. I’m sure that some of this is incorrect, and I hope we’ll all learn more at WWDC24.

Spherical Content

Imagine sitting in a swivel chair and looking straight ahead. If you tilt your head to look straight up (at the zenith), that’s 90 degrees. Likewise, if you were looking straight ahead and tilted your head all the way down (at the nadir), that’s also 90 degrees. So, your reality has a total vertical field-of-view of 90 + 90 = 180 degrees.

Sitting in that same chair, if you swivel 90 degrees to the left or 90 degrees to the right, you’re able to view a full 90 + 90 = 180 degrees of horizontal content (your horizontal field-of-view). If you spun your chair all the way around to look at the “back half” of your environment, you would spin past a full 360 degrees of content.

When we talk about immersive video, it’s common to only refer to the horizontal field-of-view (like 180 or 360) with the assumption that the vertical field-of-view is always 180. Of course, this doesn’t have to be true, because we can capture whatever we’d like, edit whatever we’d like, and playback whatever we’d like.

But when someone says something like VR180, they really mean immersive video that has a 180-degree horizontal field-of-view and a 180-degree vertical field-of-view. Similarly, 360 video is 360-degrees horizontally by 180-degrees vertically.

Projections

When immersive video is played back in a device like the Apple Vision Pro, the Meta Quest, or others, the content is displayed as if a viewer’s eyes are at the center of a sphere watching video that is displayed on its inner surface. For 180-degree content, this is a hemisphere. For 360-degree content, this is a full sphere. But it can really be anything in between; at Pixvana, we sometimes referred to this as any-degree video.

It’s here where we run into a small problem. How do we encode this immersive, spherical content? All the common video codecs (H.264, VP9, HEVC, MV-HEVC, AV1, etc.) are designed to encode and decode data to and from a rectangular frame. So how do you take something like a spherical image of the Earth (i.e. a globe) and store it in a rectangular shape? That sounds like a map to me. And indeed, that transformation is referred to as a map projection.

Equirectangular

While there are many different projection types that each have useful properties in specific situations, spherical video and images most commonly use an equirectangular projection. This is a very simple transformation to perform (it looks more complicated than it is). Each x location on a rectangular image represents a longitude value on a sphere, and each y location represents a latitude. That’s it. Because of these relationships, this kind of projection can also be called a lat/long.

Imagine “peeling” thin one-degree-tall strips from a globe, starting at the equator. We start there because it’s the longest strip. To transform it to a rectangular shape, start by pasting that strip horizontally across the middle of a sheet of paper (in landscape orientation). Then, continue peeling and pasting up or down in one-degree increments. Be sure to stretch each strip to be as long as the first, meaning that the very short strips at the north and south poles are stretched a lot. Don’t break them! When you’re done, you’ll have a 360-degree equirectangular projection that looks like this.

If you did this exact same thing with half of the globe, you’d end up with a 180-degree equirectangular projection, sometimes called a half-equirect. Performed digitally, it’s common to allocate the same number of pixels to each degree of image data. So, for a full 360-degree by 180-degree equirect, the rectangular video frame would have an aspect ratio of 2:1 (the horizontal dimension is twice the vertical dimension). For 180-degree by 180-degree video, it’d be 1:1 (a square). Like many things, these aren’t hard and fast rules, and for technical reasons, sometimes frames are stretched horizontally or vertically to fit within the capabilities of an encoder or playback device.

This is a 180-degree half equirectangular image overlaid with a grid to illustrate its distortions. It was created from the standard fisheye image further below. Watch an animated version of this transformation.

What we’ve described so far is equivalent to monoscopic (2D) video. For stereoscopic (3D) video, we need to pack two of these images into each frame…one for each eye. This is usually accomplished by arranging two images in a side-by-side or over/under layout. For full 360-degree stereoscopic video in an over/under layout, this makes the final video frame 1:1 (because we now have 360 degrees of image data in both dimensions). As described in my prior post on Encoding Spatial Video, though, Apple has chosen to encode stereo video using MV-HEVC, so each eye’s projection is stored in its own dedicated video layer, meaning that the reported video dimensions match that of a single eye.

Standard Fisheye

Most immersive video cameras feature one or more fisheye lenses. For 180-degree stereo (the short way of saying stereoscopic) video, this is almost always two lenses in a side-by-side configuration, separated by ~63-65mm, very much like human eyes (some 180 cameras).

The raw frames that are captured by these cameras are recorded as fisheye images where each circular image area represents ~180 degrees (or more) of visual content. In most workflows, these raw fisheye images are transformed into an equirectangular or half-equirectangular projection for final delivery and playback.

This is a 180 degree standard fisheye image overlaid with a grid. This image is the source of the other images in this post.

Apple’s Fisheye

This brings us to the topic of this post. As I stated in the introduction, Apple has encoded the raw frames of their immersive videos in a “fisheye” projection format. I know this, because I’ve monitored the network traffic to my Apple Vision Pro, and I’ve seen the HLS streaming manifests that describe each of the network streams. This is how I originally discovered and reported that these streams – in their highest quality representations – are ~50Mbps, HDR10, 4320×4320 per eye, at 90fps.

While I can see the streaming manifests, I am unable to view the raw video frames, because all the immersive videos are protected by DRM. This makes perfect sense, and while I’m a curious engineer who would love to see a raw fisheye frame, I am unwilling to go any further. So, in an earlier post, I asked anyone who knew more about the fisheye projection type to contact me directly. Otherwise, I figured I’d just have to wait for WWDC24.

Lo and behold, not a week or two after my post, an acquaintance introduced me to Andrew Chang who said that he had also monitored his network traffic and noticed that the Apple TV+ intro clip (an immersive version of this) is streamed in-the-clear. And indeed, it is encoded in the same fisheye projection. Bingo! Thank you, Andrew!

Now, I can finally see a raw fisheye video frame. Unfortunately, the frame is mostly black and featureless, including only an Apple TV+ logo and some God rays. Not a lot to go on. Still, having a lot of experience with both practical and experimental projection types, I figured I’d see what I could figure out. And before you ask, no, I’m not including the actual logo, raw frame, or video in this post, because it’s not mine to distribute.

Immediately, just based on logo distortions, it’s clear that Apple’s fisheye projection format isn’t the same as a standard fisheye recording. This isn’t too surprising, given that it makes little sense to encode only a circular region in the center of a square frame and leave the remainder black; you typically want to use all the pixels in the frame to send as much data as possible (like the equirectangular format described earlier).

Additionally, instead of seeing the logo horizontally aligned, it’s rotated 45 degrees clockwise, aligning it with the diagonal that runs from the upper-left to the lower-right of the frame. This makes sense, because the diagonal is the longest dimension of the frame, and as a result, it can store more horizontal (post-rotation) pixels than if the frame wasn’t rotated at all.

This is the same standard fisheye image from above transformed into a format that seems very similar to Apple’s fisheye format. Watch an animated version of this transformation.

Likewise, the diagonal from the lower-left to the upper-right represents the vertical dimension of playback (again, post-rotation) providing a similar increase in available pixels. This means that – during rotated playback – the now-diagonal directions should contain the least amount of image data. Correctly-tuned, this likely isn’t visible, but it’s interesting to note.

More Pixels

You might be asking, where do these “extra” pixels come from? I mean, if we start with a traditional raw circular fisheye image captured from a camera and just stretch it out to cover a square frame, what have we gained? Those are great questions that have many possible answers.

This is why I liken video processing to turning knobs in a 747 cockpit: if you turn one of those knobs, you more-than-likely need to change something else to balance it out. Which leads to turning more knobs, and so on. Video processing is frequently an optimization problem just like this. Some initial thoughts:

• It could be that the source video is captured at a higher resolution, and when transforming the video to a lower resolution, the “extra” image data is preserved by taking advantage of the square frame.
• Perhaps the camera optically transforms the circular fisheye image (using physical lenses) to fill more of the rectangular sensor during capture. This means that we have additional image data to start and storing it in this expanded fisheye format allows us to preserve more of it.
• Similarly, if we record the image using more than two lenses, there may be more data to preserve during the transformation. For what it’s worth, it appears that Apple captures their immersive videos with a two-lens pair, and you can see them hiding in the speaker cabinets in the Alicia Keys video.

There are many other factors beyond the scope of this post that can influence the design of Apple’s fisheye format. Some of them include distortion handling, the size of the area that’s allocated to each pixel, where the “most important” pixels are located in the frame, how high-frequency details affect encoder performance, how the distorted motion in the transformed frame influences motion estimation efficiency, how the pixels are sampled and displayed during playback, and much more.

Blender

But let’s get back to that raw Apple fisheye frame. Knowing that the image represents ~180 degrees, I loaded up Blender and started to guess at a possible geometry for playback based on the visible distortions. At that point, I wasn’t sure if the frame encodes faces of the playback geometry or if the distortions are related to another kind of mathematical mapping. Some of the distortions are more severe than expected, though, and my mind couldn’t imagine what kind of mesh corrected for those distortions (so tempted to blame my aphantasia here, but my spatial senses are otherwise excellent).

One of the many meshes and UV maps that I’ve experimented with in Blender.

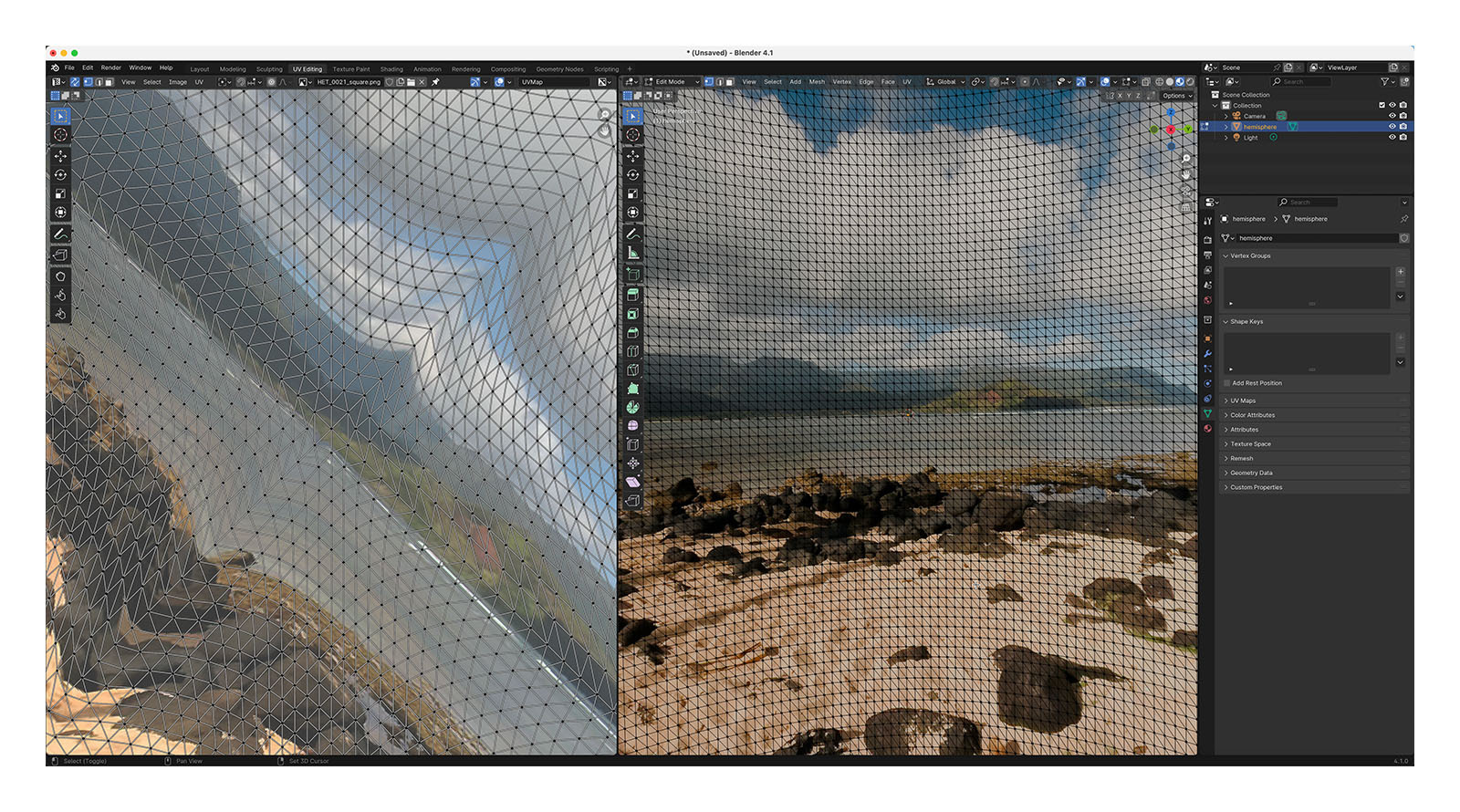
Radial Stretching

If you’ve ever worked with projection mappings, fisheye lenses, equirectangular images, camera calibration, cube mapping techniques, and so much more, Google has inevitably led you to one of Paul Bourke’s many fantastic articles. I’ve exchanged a few e-mails with Paul over the years, so I reached out to see if he had any insight.

After some back-and-forth discussion over a couple of weeks, we both agreed that Apple’s fisheye projection is most similar to a technique called radial stretching (with that 45-degree clockwise rotation thrown in). You can read more about this technique and others in Mappings between Sphere, Disc, and Square and Marc B. Reynolds’ interactive page on Square/Disc mappings.

Basically, though, imagine a traditional centered, circular fisheye image that touches each edge of a square frame. Now, similar to the equirectangular strip-peeling exercise I described earlier with the globe, imagine peeling one-degree wide strips radially from the center of the image and stretching those along the same angle until they touch the edge of the square frame. As the name implies, that’s radial stretching. It’s probably the technique you’d invent on your own if you had to come up with something.

By performing the reverse of this operation on a raw Apple fisheye frame, you end up with a pretty good looking version of the Apple TV+ logo. But, it’s not 100% correct. It appears that there is some additional logic being used along the diagonals to reduce the amount of radial stretching and distortion (and perhaps to keep image data away from the encoded corners). I’ve experimented with many approaches, but I still can’t achieve a 100% match. My best guess so far uses simple beveled corners, and this is the same transformation I used for the earlier image.

It’s also possible that this last bit of distortion could be explained by a specific projection geometry, and I’ve iterated over many permutations that get close…but not all the way there. For what it’s worth, I would be slightly surprised if Apple was encoding to a specific geometry because it adds unnecessary complexity to the toolchain and reduces overall flexibility.

While I have been able to playback the Apple TV+ logo using the techniques I’ve described, the frame lacks any real detail beyond its center. So, it’s still possible that the mapping I’ve arrived at falls apart along the periphery. Guess I’ll continue to cross my fingers and hope that we learn more at WWDC24.

Conclusion

This post covered my experimentation with the technical aspects of Apple’s fisheye projection format. Along the way, it’s been fun to collaborate with Andrew, Paul, and others to work through the details. And while we were unable to arrive at a 100% solution, we’re most definitely within range.

The remaining questions I have relate to why someone would choose this projection format over half-equirectangular. Clearly Apple believes there are worthwhile benefits, or they wouldn’t have bothered to build a toolchain to capture, process, and stream video in this format. I can imagine many possible advantages, and I’ve enumerated some of them in this post. With time, I’m sure we’ll learn more from Apple themselves and from experiments that all of us can run when their fisheye format is supported by existing tools.

It’s an exciting time to be revisiting immersive video, and we have Apple to thank for it.

As always, I love hearing from you. It keeps me motivated! Thank you for reading.